Traveling Salesman Problem in logistics – calculate the impossible
It is well known that thanks to the development of Information Technology (IT), companies are achieving better and better sales results, not to mention that they can function at all thanks to software solutions. Furthermore, people can handle more and more matters or work through the Internet. However, not everyone knows that even computer science has its limits and cannot provide an exact answer to everything.
Within the field of computer science, there have been issues and problems for years that have not yet had efficient and fundamental solutions proposed. One of them is the optimization problem called the traveling salesman problem, which is closely associated with the TSL (Transport Spedition Logistics) industry. Read on to learn more about it. Perhaps you will be the lucky one to solve this problem.
How did the “Traveling Salesman Problem” come about?
It is difficult to pinpoint the person who first announced the difficulty in indicating a set of instructions for solving the traveling salesman problem (TSP). The first mentions of it date back to the 1830s, and the first attempts to solve it were made about 100 years later when trying to find the optimal route for a school bus. We will leave the analysis of the problem based on complex mathematical laws and expressions to scientists. That’s why I will focus on its essence by presenting it in an easily understandable way.
What is the TSP problem?
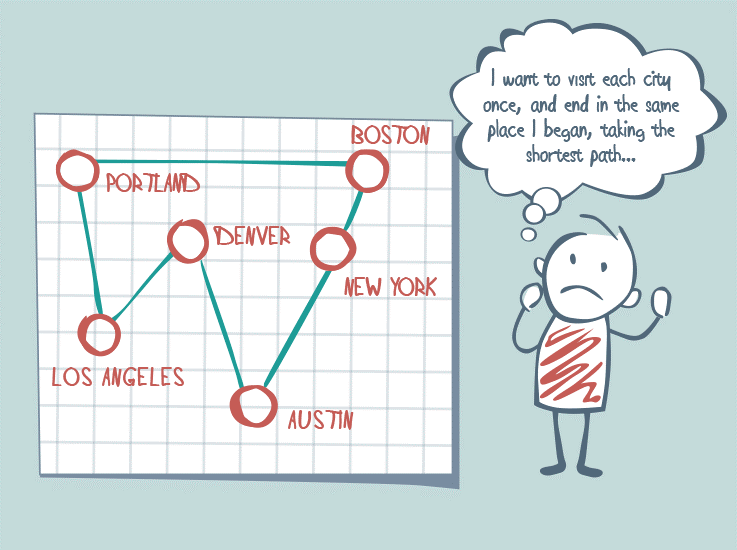
Let’s assume there is a courier who starts and ends his work in Boston. One day, he has to deliver packages to addresses in New York, Denver, Los Angeles, Austin, Portland, and Chicago. The traveling salesman problem consists of finding the shortest route that allows the courier to visit all these cities. It doesn’t have to be just about the length of the route, as it can also focus on finding the cheapest or fastest way. In our example, the number of possible routes is 5040.
How do companies deal with the TSP problem?
If we are looking for the shortest route for several cities, finding the optimal solution can take seconds or a few minutes on an ordinary computer. However, when we talk about, for example, 52 cities, various algorithms, and parallel and distributed computing are used to find approximate solutions, sufficient for logistics, because checking all possible routes is practically impossible. You probably won’t be surprised that artificial intelligence (AI) plays a role in this.
Applications of the Traveling Salesman Problem
The traveling salesman problem has many practical applications. The main one, and the reason for writing this article, is the optimization of routes for fleets of vehicles, ships, or airplanes, minimizing costs and delivery time. Another application is the planning of routes for robots in warehouses or logistics centers. TSP is also used in the design of telecommunication networks to ensure optimal signal quality and minimize costs.
We will help you optimize your loading
While we may not be able to solve the traveling salesman problem and find the optimal route for any number of cities, we have a program for cargo loading planning called EasyCargo. In addition to creating an optimal plan for the arrangement of goods (you can group them by unloading locations) and load distribution, it allows you to generate reports in Excel or PDF format. Even a public link for collaboration work with colleagues on cargo loads is available.
Additionally, you can integrate EasyCargo with your company software or other programs such as the FleetUp telemetry system using our API. You can learn more about its details at this link.

One could actually say that for the TSL industry, the traveling salesman problem is slowly becoming less of a worry thanks to the development of artificial intelligence and Big Data. All kinds of delivery route optimization software offer a route that does not deviate significantly from the most favorable one and dynamically adjusts it in real time depending on the conditions on the roads.
Good luck with proposing an algorithm that can find the optimal route for any number of cities in polynomial time!




